Raw data is always murky; before it can be analyzed, it needs to be inspected, cleansed, and prepared. Data may be incomplete, inaccurate, inconsistent, or erratic. Outliers are a common anomaly in data analysis. An outlier occurs when the value of one or more data points falls unusually far from the values of most other data points. Outliers, if not corrected, can dramatically skew the outcomes of your analysis, causing you to make incorrect conclusions and/or predictions. In this post, we will explain why outliers occur; illustrate how outliers can impact your results; discuss how to detect outliers; and provide strategies commonly used to correct for outliers.
Reasons Outliers Occur
Outliers can occur for many reasons, with incorrect data entry being a likely culprit. Outliers can also occur because the sample we have drawn can have unique characteristics not common in other possible samples, or the population itself does not follow a normal distribution. And, sometimes, outliers just occur naturally.
Let’s assume a local bank wants to determine the average income of car loan applicants, so it randomly selects 10 applications, and pulls their stated incomes:
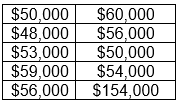
Notice the last observation. All the other values range from $48,000 to $60,000, but the last observation is much greater: $154,000.
It may well be that this applicant has an income of $154,000 per year; that would be a naturally occurring outlier. Or the applicant’s income was just $54,000 and the data was entered erroneously as $154,000. What if the applicant included his/her income from all sources: wages, alimony, investment income, etc., and all the others just listed their wage income? That would be a measurement error. Or maybe the bank is in a remote area, and it’s the only lender in the immediate vicinity, so everyone, regardless of income, applies there. Then the $154,000 income would not just be a naturally occurring outlier but would also be indicative of an outlier due to sampling and/or population distribution.
How Outliers Impact Results
If outliers are not addressed, they can distort your analysis greatly and lead to incorrect findings and bad business decisions. Certain statistical measures are more sensitive to outliers than others. Outliers have a strong effect on the mean (average) and the standard deviation (which measures how spread out the data is), but little or none on the median (the middle value of the data set).
If, for example, the last observation was supposed to be just $54,000, then the mean and median incomes of these 10 applicants would each be $54,000, and the standard deviation would be $3,916, suggesting that the applicant incomes are largely similar.
However, if this $154,000 is indeed correct (or incorrect and uncorrected), the mean income would be $64,000 and the standard deviation would be $31,864, suggesting a considerable amount of spread. The median increases slightly, to $55,000. The fact that the mean income is much greater than the median income indicates the average is skewed.
This skewed data can cause problems. If the bank relies solely on the mean income of the applicant in making decisions, it might design an auto loan promotion targeting high income households, which may then fall short because most of its applicants are lower income. On the flip side, when the bank must report its efforts in low income lending to regulators, the mean income alone will suggest that its borrowers have higher incomes than they actually do, and the bank could face fines and/or other repercussions for noncompliance.
Outliers should rarely, if ever, be ignored.
Detecting Outliers
Outliers can be detected in several ways, one of which is simply calculating the descriptive statistics, which was done above. How spread out is the data? The range will indicate that: $48,000 to $154,000, in this example. But just because the range is wide doesn’t mean the data has outliers. The next step is to look at the mean, median, and standard deviation. If the mean and the median are close, that’s a good – but not reliable – indicator that there are no outliers. The standard deviation is a better indicator: if the standard deviation is large compared to the mean – or greater than the mean – outliers are likely present.
Visual inspection of the data is another way to check for outliers. Visual inspection methods include histograms, box plots, and scatterplots. These methods are a little more difficult to explain and will be covered in a later blog post.
Logical detection is another way to identify outliers. Simply put, does a particular value make logical sense? For example, if body temperatures were being recorded, a temperature of 130°F is illogical, since it would be terminal to the patient; it’s more likely the patient’s temperature is 103°F, and the numbers were transposed.
Strategies for Handling Outliers
Once you’ve detected outliers, you need to decide how you will address them. You should first ask whether those data points are accurate. Check the original source of the data and correct any values that are incorrect.
Your second consideration should be the data mining algorithm you intend to use. Association-based techniques, such as decision trees, are often robust when outliers are present, since they concentrate on the rank, rather than the actual value of the number. However, outliers can seriously disrupt neural networks and regression analyses.
In the case of the decision tree algorithm, you likely don’t need to do anything to the outliers. For the other algorithms, your third consideration will be how to adjust the outliers in some form or another; approaches include:
- Analyze the outlier(s) separately. It may well be that these outliers are truly exceptional. In the bank example, the applicant with the $154,000 annual income might be the wealthiest person in an area with a small population, so the bank should analyze the other 9 applicants for its main analysis and think of other ways to address its wealthier applicant.
- Eliminate the record.If outliers are significantly out of range, you might just exclude them from your analysis altogether, but this can bias both your sample and your results, especially if the sample is small. Although the sample in the bank example is small, eliminating the highest value introduces little bias since all the other values are clustered close together.
- Categorize, or bin, the values. This places values in ranges, so outliers will be classified appropriately: in the bank example above, the bank can create a binary variable, where a value of 1 can represent “More than $54,000” and a value of 0 can represent “$54,000 or less.” In other examples, an analyst can break values into “low,” “medium,” or “high.” Still, values can be binned “Less than $15,000,” “$15,001-$30,000,” and so on.
- Transform the outlying values. Transformation can take on many forms, including capping the value of the outlier to minimum or maximum value; predicting a likelier value using regression analysis or some other imputation method; substituting the average of all the other non-outlier values; or taking the natural log of all the values and using that in your analysis instead. Note, however, that transforming your variables, especially by using the natural log, can also transform your analysis.
There is no perfect way to handle outliers; the process is as much an art as it is a science. The most effective strategy for handling outliers is contingent on your domain knowledge: how the data was collected and entered; your company’s business rules; and the objectives of your analysis. Your domain knowledge can help you identify whether and why an outlier occurred; assess its impact; and determine the best approach to address it. Outliers are a regular occurrence in data sets and shouldn’t be ignored, lest they distort your findings.

